Improving paleosol carbonate based estimates of ancient atmospheric CO2

Dan Breecker, Department of Geological Sciences, The University of Texas at Austin

Summary

The stable carbon isotope composition of calcium carbonate precipitated in soils (pedogenic carbonate) is controlled in part by the concentration of atmospheric CO₂ ([CO₂]_atm) during soil formation. Paleosol carbonates that escape alteration during burial diagenesis therefore preserve records of ancient [CO₂]_atm. However, in order to accurately reconstruct [CO₂]_atm we must be able to accurately interpret the stable carbon isotope composition of pedogenic carbonate (δ¹³C_pc). Other variables such as temperature, moisture and soil CO₂ concentration that influence both calcite solubility and δ¹³C_pc values vary greatly on a seasonal basis, especially in soils where pedogenic carbonate forms. We must therefore ask: what does the stable isotope composition of pedogenic carbonate record? The following discussion reviews recent advances in understanding the conditions under which calcium carbonate forms in modern soils, some of the implications of these findings and future research directions for further improvement of paleosol carbonate-based reconstructions of atmospheric CO₂.

Introduction

Paleosol carbonate records a wealth of information about ancient terrestrial environments. Modern pedogenic carbonate occurs, with few exceptions, only in climates with pronounced seasonal variations in precipitation minus evaporation. Therefore the sole presence of pedogenic carbonate in paleosols is an indicator of seasonal dryness and limited soil leaching. The depth of carbonate-bearing soil horizons is related to mean annual precipitation (Arkley, 1963; Gile, 1977; Jenny and Leonard, 1935; Retallack, 1994, 2005) although the significance of this relationship has been challenged (Royer, 1999) and it has been proposed that soil order-specific relationships are required (Nordt et al., 2006). The oxygen isotope composition of pedogenic carbonate is controlled by the oxygen isotope composition of precipitation (Cerling, 1984) and has been used to reconstruct the elevation history of large plateaus (e.g. Currie et al., 2005; Garzione et al., 2000; Ghosh et al., 2006b) and paleoatmospheric circulation (e.g. Amundson et al., 1996). The carbon isotope composition of pedogenic carbonate provides a record of vegetation in the past (Cerling, 1984, 1999) and has been used in numerous paleoecologic studies (e.g. Cerling and Hay, 1986; Fox and Koch, 2003; Kaakinen et al., 2006; Koch et al., 1995; Quade et al., 1989). Of particular interest in geochemistry, the carbon isotope composition of paleosol carbonate has also been used to reconstruct Phanerozoic atmospheric pCO₂ (e.g. Ekart et al., 1999 and references therein; Ghosh et al., 2001; Lee, 1999; Montañez et al., 2007; Nordt et al., 2002, 2003; Prochnow et al., 2006; Robinson et al., 2002). Quantifying [CO₂]_atm through geologic time is widely important in studies of the geologic carbon cycle, the evolution of organisms, mass extinctions, and Earth's climate. This paper describes recent and future efforts to improve [CO₂]_atm estimates using pedogenic carbonate.

The paleosol carbonate CO₂ barometer

Figure 1. A graphical representation of the lever rule as applied to the paleosol barometer. δ¹³C_r* represents the diffusion-modified δ¹³C value of the soil-derived endmember and equals 1.0044δ¹³C_r + 4.4. The magnitude of [CO₂]_atm and S(z) are proportional to the distances along the lever, or differences in δ values, as labeled. Equation 1 can be written directly from the relationship shown. Figure 1

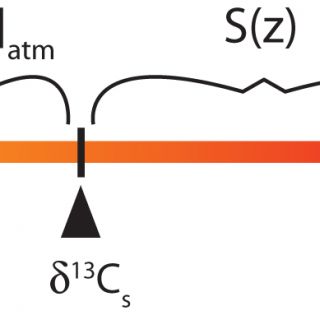
The paleosol carbonate CO₂ barometer or ‘paleosol barometer' for short, although this name does not distinguish the technique from the similar but independent ‘paleosol goethite CO₂ barometer' (Yapp and Poths, 1992), was developed by Thure Cerling in the 1990s. Cerling (1991; 1999) understood that CO₂ in soil pore spaces is a mixture between atmospheric and soil-derived (from autotrophic and heterotrophic soil respiration) components and recognized that if soil carbonate forms in carbon isotope equilibrium with soil CO₂ then the δ¹³C value of soil carbonate is a function of the relative magnitude of the atmospheric and soil-respired components and their respective δ¹³C values. The mass balance relationship is pictured graphically using the lever rule in Figure 1, from which it can be seen that:

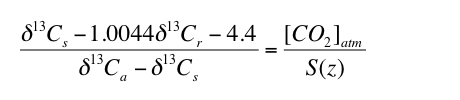1)

where S(z) is the soil-respired component of total CO₂ in the soil (i.e. [CO₂]_soil = S(z) + [CO₂]_atm) at depth z, δ¹³C is the carbon isotope composition in standard delta notation, s, r and a refer to soil CO₂, soil-respired CO₂ and atmospheric CO₂, respectively, and the coefficient 1.0044 and the constant 4.4 derive from the difference in diffusivity between ¹³CO₂ and ¹²CO₂. The value of δ¹³C_s in equation 1 is determined by using the temperature dependent carbon isotope fractionation factor (e.g. Romanek et al., 1992) to calculate the δ¹³C value of CO₂ in equilibrium with the measured δ¹³C value of paleosol carbonate (δ¹³C_pc). The δ¹³C value of soil carbonate can therefore, in appropriate soils, be used to calculate [CO₂]_atm using the following equation which is simply rearranged from equation 1 (Cerling, 1999):

"

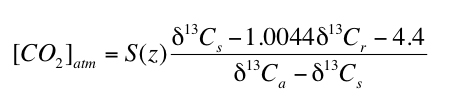2)

Equation 2 has been used to reconstruct [CO₂]_atm for many time periods during the past 400 million years of Earth's history (e.g. Ekart et al., 1999).

The formation of pedogenic carbonate

In order to assign values to the variables on the right hand side of equation 2, it is typically assumed that paleosol carbonate formed at temperatures and soil CO₂ concentrations characterized by mean growing season conditions observed in modern soils (Cerling, 1991). However, recent work indicates that pedogenic carbonate does not form during mean growing season conditions, but instead forms during droughts (Breecker et al., 2009). In that study, the δ¹³C values of soil CO₂ in modern soils from New Mexico, USA were generally lower than values in equilibrium with soil carbonate and only approached equilibrium values after an extended two month drought (typical of spring in New Mexico). The timing of carbon isotope equilibrium between soil CO₂ and soil carbonate was interpreted to identify the timing of carbonate formation. This interpretation requires the assumption that soil carbonate forms in carbon isotope equilibrium with soil CO₂, which is theoretically justified (Cerling and Quade, 1993), but remains to be experimentally or empirically demonstrated. However, the interpretation based on isotope equilibrium that pedogenic carbonate forms during warm, dry episodes is strongly supported by thermodynamic considerations: precipitation of carbonate in soils is driven by increasing temperature, increasing Ca²⁺ activity as a result of evapotranspiration, and decreasing soil pCO₂, caused by deceasing soil respiration rates as a result of water stress on plants and soil microorganisms.

A recently developed geothermometer that is based on the concentration of ¹³C-¹⁸O bonds in calcite (the ‘clumped isotope thermometer') (Ghosh et al., 2006a; Schauble et al., 2006) is useful for investigating pedogenic carbonate formation. The formation temperatures determined using the clumped isotope thermometer of modern pedogenic carbonates collected at depths in excess of 50 cm are approximately equal to the mean air temperature during the warmest consecutive three months of the year (Passey et al., 2010). These high temperatures at depth during carbonate formation likely result from radiative heating of the soil surface as the soil dries and latent heat flux decreases and support the conclusion of Breecker et al (2009).

The conclusion that soil carbonate forms under conditions of water stress suggests that the S(z) values typically used in the paleosol barometer are higher than those appropriate for carbonate formation, which has resulted in substantial overestimation of paleoatmospheric CO₂ (Breecker et al., 2010). Revised paleoatmospheric CO₂ concentrations, determined using a more realistic S(z) value that is based on the study of modern soils, suggest that Earth's maximum persistent atmospheric CO₂ levels during the past 400 million years were in the range of 1000 ± 200 ppmV and that CO₂ levels similar to those predicted for the end of this century (800-1000 ppmV, estimated by the IPCC using SRES emission scenario A2 (Meehl et al., 2007)) may have forced Mesozoic greenhouse climate warmth (Breecker et al., 2010). The importance of this conclusion demands it be rigorously tested.

Breecker et al. (2010) used a single S(z) value for all paleosols which probably results in accurate estimates of mean [CO₂]_atm calculated from large numbers of paleosols, but is probably not appropriate for every individual paleosol. Determining S(z) values that are appropriate for individual paleosols is a crucial step in improving the accuracy and temporal resolution of [CO₂]_atm records. Progress on this front was made by a recent study in which S(z) values varied with paleosol morphology (Montañez et al., 2007). It has been reported that S(z) values correlate with, and may partly control, the depth from the soil surface to the carbonate-bearing horizon (Bk horizon), for a small but geographically diverse sample of modern soils (Retallack, 2009). This type of relationship may eventually be useful for assigning S(z) values to individual paleosols if it is calibrated for the seasonal timing of carbonate formation and if other variables that influence the depth to the Bk horizon (e.g. soil texture, parent material) can be accounted for.

Uncertainty of paleoatmospheric CO₂ estimates

Figure 2. Monte Carlo simulations of the uncertainty of calculated atmospheric CO₂ concentrations. 10,000 values were randomly selected from each of the following normal distributions (mean ± standard deviation) and used to calculate atmospheric CO₂ concentrations with equation 2: δ¹³C_r = -26 ± 1‰, δ¹³C_a = -6.5 ± 1‰, temperature = 25 ± 5°C, S(z) = 1000, 2500 or 5000 ± 50%. A range of mean δ¹³C_pc values between -3 and -12‰(± 0.5‰) were used to calculate a range of mean atmospheric CO₂ concentrations (x-axis) for each mean S(z) value. The total uncertainty was estimated by calculating the standard deviation (1σ) of each set of 10,000 atmospheric CO₂ concentrations and is expressed as a percentage of the mean calculated value of [CO₂]_atm. Figure 2

Figure 3. Monte Carlo simulations of the effect of each variable in equation 2 on the total uncertainty. The y-axis is the ratio of the uncertainty calculated when the value of one of the variables (labeled on each plot) is known exactly to the total uncertainty from Figure 2. Figure 3

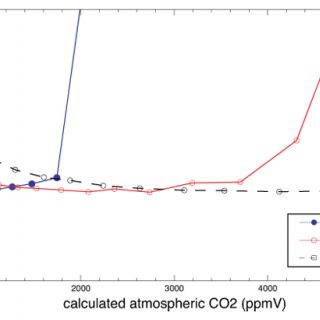
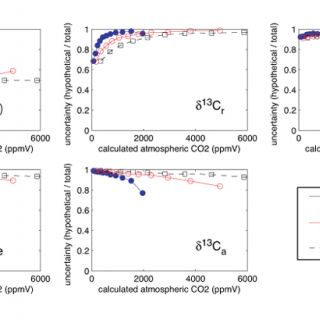
Here I use Monte Carlo simulations to investigate the how uncertainty in each of the variables on the right hand side of equation 2 (including temperature, which is used to calculate δ¹³C_s) influences uncertainty in the calculated values of [CO₂]_atm. Figure 2 is a plot of the estimated total uncertainty of [CO₂]_atm calculated using equation 2. Figure 3 illustrates the degree to which the total uncertainty is reduced if the value of one of the variables in equation 2 is known exactly.

Simulated uncertainties vary with the calculated values of [CO₂]_atm (Figures 2 & 3). The total uncertainties decrease as values of [CO₂]_atm approach values of S(z) (Figure 2). When S(z) ≈ [CO₂]_atm (the zones of minimum total uncertainty in Figure 1) calculated uncertainties are also more sensitive to S(z) than they are to any of the other variables in equation 2 (i.e. exact values of S(z) reduce uncertainty more than exact values of any of the other variables do) (Figure 3). Sensitivity to δ¹³C_r increases as the ratio of mean values [CO₂]_atm/S(z) decreases and sensitivity to δ¹³C_a increases as [CO₂]_atm/S(z) increases (Figure 3). These results are expected based on the lever rule: the relative magnitude of [CO₂]_atm and S(z) is impacted more by changes on the short end than on the long end of the lever. The decreases in uncertainty resulting from knowing exact values of temperature and δ¹³C_pc are small (Figure 3) because the value of δ¹³C_s is relatively insensitive to temperature and the value of δ¹³C_pc is generally well constrained (i.e. δ¹³C_pc was assigned a small error in this analysis). Therefore, the clumped isotope thermometer is not expected to improve the uncertainty of [CO₂]_atm calculated using the paleosol barometer, although it is promising for the quantification of soil and maximum air paleotemperatures (Passey et al., 2010).

The results of the Monte Carlo simulations indicate that selecting paleosols for which appropriate S(z) values are similar to contemporaneous [CO₂]_atm values will improve uncertainty. Inspecting Figure 2 indicates that the total uncertainty is less than 80% of the average calculated value of [CO₂]_atm when [CO₂]_atm/S(z) is between the values of 0.3 and 1.8. Total uncertainty increases sharply for [CO₂]_atm/S(z) outside this range (Figure 2). Therefore, using equation 1, paleosols that will result in the lowest uncertainty can be identified, without needing to assume values for [CO₂]_atm or S(z), by assuring that the following holds true for the applicable δ¹³C values:

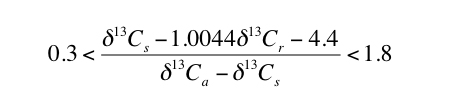3)

The results of the Monte Carlo simulations also indicate that better estimates of δ¹³C_r may be required to improve estimates for time periods when [CO₂]_atm was below ~500 ppmV. This is especially true if water stress is found to have a substantial impact on δ¹³C_r values in calcic soils as hypothesized below. These conclusions are intended to motivate and direct future research.

Calibrating the barometer

The paleosol carbonate CO₂ barometer can be calibrated by studying modern calcic soils. Application of the barometer to Holocene soils (for which the correct atmospheric CO₂ concentrations are preindustrial values) is a reasonable but somewhat blind calibration technique in that it does not address process nor does it allow independent calibration of each variable in equation 2. Monitoring seasonal variation in variables such as soil temperature, soil moisture, soil CO₂ concentration and the stable isotope composition of soil CO₂ will help establish the timing and mechanism of carbonate formation and help assign values for T, δ¹³C_r and S(z) that are appropriate in equation 2. The discussion of model sensitivity above indicates that efforts are most worthwhile spent on improving estimates of S(z) and δ¹³C_r. Interestingly, it appears that there may be room for improvement in both of these variables.

Soil CO₂ concentrations vary greatly among different soils and seasonally within the same soil. S(z) values that correspond to carbonate formation have not been widely identified. Ongoing work on a variety of modern soils will help refine S(z) values appropriate for different paleosol types. Vertisols (soils in which shrinking and swelling of clays dominate morphological development) and soils with vertic properties are commonly preserved in the geologic record. Vertisols Therefore, my group at UT and a group at Baylor University led by Drs. Steve Driese and Lee Nordt are together currently studying soil CO₂ and pedogenic carbonate in modern Vertisols from central and south Texas. These Vertisols are particularly good modern analogs for many paleo-Vertisols used to reconstruct ancient [CO₂]_atm (e.g. Mora and Driese, 1999; Mora et al., 1996; Nordt et al., 2002, 2003). Our hypothesis is that cracking of these smectite-rich soils upon drying opens conduits for the release of CO₂ from the soil, resulting in a large decrease in soil CO₂ concentration, which in turn drives calcite precipitation. We suspect that decreasing soil respiration rates, increased pore space volume, increased diffusivity and barometric pumping through cracked soil all influence the dynamics of soil CO₂ in Vertisols. Understanding the processes involved in carbonate formation and soil CO₂ variations may help establish proxies for S(z) and δ¹³C_r.

Values for δ¹³C_r in equation 2 are typically assumed to equal the δ¹³C value of well-preserved, contemporaneous terrestrial organic material (e.g. Montañez et al., 2007; Nordt et al., 2002), or are calculated from the δ¹³C value of contemporaneous marine carbonate assuming a constant carbon isotope fractionation between the ocean and the atmosphere and between the atmosphere and vegetation (e.g. Ekart et al., 1999; Nordt et al., 2003). However, it is well known that there is a wide range in the δ¹³C value of C₃ plants (Deines, 1980), resulting at least in part from the effect of water stress on the magnitude of photosynthetic discrimination (Farquhar et al., 1989). Water stress, which tends to occur in the seasonally dry climates in which pedogenic carbonates form, can substantially increase the δ¹³C values of plants and can even result in substantial (~2‰) differences in the δ¹³C value of the leaves of individual species growing along local soil moisture gradients (e.g. Ehleringer and Cooper, 1988). Terrestrial organic materials are typically well-preserved where they were protected from degradation in rapidly aggrading sediments or anoxic, water-saturated environments such as swamps. Unfortunately this creates a preservation bias toward plant material that is less water stressed when compared with the vegetation that was probably growing in calcic soils. Furthermore, approximately half of the CO₂ respired in soils is generated in the rhizosphere (root zone) (Hanson et al., 2000) where the substrate consists largely of recently assimilated carbon (Ekblad and Högberg, 2001; Högberg et al., 2001). Therefore, δ¹³C values of rhizosphere-respired CO₂ vary seasonally and are highest when vegetation is water stressed and pedogenic carbonate is forming. These considerations suggest that the δ¹³C value of respired CO₂ in calcic paleosols was higher than the δ¹³C value of well-preserved organic matter in sedimentary successions. However, there is considerable direct evidence for a kinetic isotope fractionation during microbial decomposition of organic matter, which results in production of ¹³C-depleted CO₂ (e.g. Blair et al., 1985; Mary et al., 1992) and therefore may somewhat compensate for the moisture-related effects described above. Finding a proxy for δ¹³C_r values that correspond to the seasonal timing of carbonate formation is a challenge for future research. A proxy for δ¹³C_r would help improve estimates of low atmospheric CO₂ concentrations during Earth's past, which are particularly important for determining the threshold CO₂ concentrations for continental glaciation (Royer, 2006).

Concluding Remarks

Soils are complicated natural systems. Simplifying our view of soils so that it is necessary and sufficient for the accurate interpretation of paleosols constitutes an ongoing challenge. Previous research has made great strides toward this end as evidenced by the emerging consensus among different techniques for reconstructing ancient [CO₂]_atm. The discussion above is intended to build on previous work by highlighting certain complexities that may be worth considering in future applications of the paleosol carbonate CO₂ barometer. Process-based proxy calibration studies can provide uniformitarian insight and are one way forward that should be encouraged.

Acknowledgements

I thank T. Cerling for inspiration, Z. Sharp, L. McFadden and J. Quade for their outstanding mentorship and G. Davidson for a helpful review.

References

Amundson, R., Chadwick, O., Kendall, C., Wang, Y., and DeNiro, M., 1996, Isotopic evidence for shifts in atmospheric circulation patterns during the late Quaternary in mid-North America: Geology, v. 24, p. 23-26.

Arkley, R.J., 1963, Calculation of carbonate and water movement in soil from climatic data: Soil Science, v. 96, p. 239-248.

Blair, N., Leu, A., Muñoz, E., Olsen, J., Kwong, E., and des Marais, D., 1985, Carbon isotopic fractionation in heterotrophic microbial metabolism: Applied and Environmental Microbiology, v. 50, p. 996-1001.

Breecker, D., Sharp, Z.D., and McFadden, L., 2009, Seasonal bias in the formation and stable isotope composition of pedogenic carbonate in modern soils from central New Mexico, USA: Geological Society of America Bulletin, v. 121, p. 630-640.

Breecker, D.O., Sharp, Z.D., and McFadden, L.D., 2010, Atmospheric CO₂ concentrations during ancient greenhouse climates were similar to those predicted for A.D. 2100.: Proceedings of the National Academy of Sciences of the United States of America, v. 107, p. 576-580.

Cerling, T.E., 1984, The stable isotopic composition of modern soil carbonate and its relationship to climate: Earth and Planetary Science Letters, v. 71, p. 229-240.

-, 1991, Carbon dioxide in the atmosphere: Evidence from Cenozoic and Mesozoic paleosols: American Journal of Science, v. 291, p. 377-400.

-, 1999, Stable carbon isotopes in palaeosol carbonates, in M. Thiry, R.S.-C., ed., Palaeoweathering, palaeosurfaces and related continental deposits. Special Publication of the International Association of Sedimentologists, Volume 27, p. 43-60.

Cerling, T.E., and Hay, R.L., 1986, An isotopic study of paleosol carbonates from Olduvai Gorge: Quaternary Research, v. 25, p. 63-78.

Cerling, T.E., and Quade, J., 1993, Stable carbon and oxygen isotopes in soil carbonates, in Swart, P.K., Lohmann, K.C., McKenzie, J., and Savin, S., eds., Climate Change in Continental Isotopic Records: Geophysical Monograph 78, American Geophysical Union, p. 217-231.

Currie, B.S., Rowley, D.B., and Tabor, N.J., 2005, Middle Miocene paleoaltimetry of southern Tibet: Implications for the role of mantle thickening and delamination in the Himalayan orogen: Geology, v. 33, p. 181-184.

Deines, P., 1980, The isotopic composition of reduced organic carbon, in Fritz, P., and Fontes, J.C., eds., Handbook of Environmental Isotope Geochemistry, Volume 1: Amsterdam, Elsevier, p. 329-406.

Ehleringer, J.R., and Cooper, T.A., 1988, Correlations between carbon isotope ratio and microhabitat in desert plants: Oecologia, v. 76, p. 562-566.

Ekart, D.D., Cerling, T.E., Montañez, I.P., and Tabor, N.J., 1999, A 400 million year carbon isotope record of pedogenic carbonate: Implications for paleoatmospheric carbon dioxide: American Journal of Science, v. 299, p. 805-827.

Ekblad, A., and Högberg, P., 2001, Natural abundance of ¹³C in CO₂ respired from forest soils reveals speed of link between tree photosynthesis and root respiration: Oecologia, v. 127, p. 305-308.

Farquhar, G.D., Ehleringer, J.R., and Hubick, K.T., 1989, Carbon isotope discrimination and photosynthesis: Annual Review of Plant Physiology and Plant Molecular Biology, v. 40, p. 503-537.

Fox, D., and Koch, P.L., 2003, Tertiary history of C₄ biomass in the Great Plains, USA: Geology, v. 31, p. 809-812.

Garzione, C.N., Quade, J., DeCelles, P.G., and English, N.B., 2000, Predicting paleoelevation of Tibet and the Himalaya from δ¹⁸O vs. altitude gradients in meteoric water across the Nepal Himalaya: Earth and Planetary Science Letters, v. 183, p. 215-229.

Ghosh, P., Adkins, J., Affek, H., Balta, B., Guo, W., Schauble, E.A., Schrag, D., and Eiler, J.M., 2006a, ¹³C-¹⁸O bonds in carbonate minerals: a new kind of paleothermometer: Geochimica et Cosmochimica Acta, v. 70, p. 1439-1456.

Ghosh, P., Garzione, C.N., and Eiler, J.M., 2006b, Rapid uplift of the Altiplano revealed through ¹³C-¹⁸O bonds in paleosol carbonates: Science, v. 311, p. 511-515.

Ghosh, P., Ghosh, P., and Bhattacharya, S.K., 2001, CO₂ levels in the late Palaeozoic and Mesozoic atmosphere from soil carbonate and organic matter, Satpura basin, Central India: Palaeogeography, Palaeoclimatology, Palaeoecology, v. 170, p. 219-236.

Gile, L.H., 1977, Holocene soils and soil-geomorphic relations in a semiarid region of southern New Mexico: Quaternary Research, v. 7, p. 112-132.

Hanson, P.J., Edwards, N.T., Garten, C.T., and Andrews, J.A., 2000, Separating root and soil microbial contribution to soil respiration: A review of methods and observations: Biogeochemistry, v. 48, p. 115-146.

Högberg, P., Nordgren, A., Buchmann, N., Taylor, A.F.S., Ekblad, A., Högberg, M.N., Nyberg, G., Ottosson-Löfvenius, M., and Read, D.J., 2001, Large scale forest girdling shows that current photosynthesis drives soil respiration: Nature, v. 411, p. 789-792.

Jenny, H.J., and Leonard, C.D., 1935, Functional relationships between soil properties and rainfall: Soil Science, v. 38, p. 363-381.

Kaakinen, A., Sonninen, E., and Lunkka, J.P., 2006, Stable isotope record in paleosol carbonates from the Chinese Loess Plateau: Implications for late Neogene paleoclimate and paleovegetation: Palaeogeography, Palaeoclimatology, Palaeoecology, v. 237, p. 359-369.

Koch, P.L., Zachos, J.C., and Dettman, D.L., 1995, Stable isotope stratigraphy and paleoclimatology of the Paleogene Bighorn Basin (Wyoming, USA): Palaeogeography, Palaeoclimatology, Palaeoecology, v. 115, p. 61-89.

Lee, Y.I., 1999, Stable isotopic composition of calcic paleosols of the early Cretaceous Hasandong Formation, southeatern Korea: Palaeogeography, Palaeoclimatology, Palaeoecology, v. 150, p. 123-133.

Mary, B., Mariotti, A., and Morel, J.L., 1992, Use of ¹³C variations at naural abundance for studying the biodegradation of root mucilage, roots an glucose in soil: Soil Biology and Biochemistry, v. 24, p. 1065-1072.

Meehl, G.A., Stocker, T.F., Collins, W.D., Friedlingstein, P., Gaye, A.T., Gregory, J.M., Kitoh, A., Knutti, R., Murphy, J.M., Noda, A., Raper, S.C.B., Watterson, I.G., Weaver, A.J., and Zhao, Z.-C., 2007, Global Climate Projections, in Solomon, S., Qin, D., Manning, M., Chen, Z., Marquis, M., Averyt, K.B., Tignor, M., and Miller, H.L., eds., Climate Change 2007: The Physcial Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change: Cambridge, Cambridge Univ. Press, p. 747-845.

Montañez, I.P., Tabor, N.J., Niemeler, D., DiMichele, W.A., Frank, T.D., Fielding, C.R., Isbell, J.L., Birgenheier, L.P., and Rygel, M.C., 2007, CO₂-forced climate and vegetation instability during late Paleozoic deglaciation: Science, v. 315, p. 87-91.

Mora, C.I., and Driese, S.G., 1999, Palaeoclimatic significance and stable carbon isotopes of Paleozoic red bed paleosols, Appalachain Basin, USA and Canada, in Thiry, M., and Simon-Coinçon, R., eds., Palaeoweathering, Palaeosurfaces and Related Continental Deposits: International Association of Sedimentologists Special Publication No. 27, p. 61-84.

Mora, C.I., Driese, S.G., and Colarusso, L.A., 1996, Middle to Late Paleozoic atmospheric CO₂ levels from soil carbonate and organic matter: Science, v. 271, p. 1105-1107.

Nordt, L., Atchley, S., and Dworkin, S.I., 2002, Paleosol barometer indicates extreme fluctuations in atmospheric CO₂ across the Creatceous-Tertiary boundary: Geology, v. 30, p. 703-706.

-, 2003, Terrestrial evidence for two greenhouse events in the latest Cretaceous: GSA Today, v. 13, p. 4-9.

Nordt, L., Orosz, M., Driese, S.G., and Tubbs, J., 2006, Vertisol carbonate properties in relation to mean annual precipitation: Implications for paleoprecipitation estimates: Journal of Geology, v. 114, p. 501-510.

Passey, B.H., Levin, N.E., Cerling, T.E., Brown, F.H., and Eiler, J.M., 2010, High temperature environments of human evolution in East Africa based on bond ordering in paleosol carbonates: Proceedings of the National Academy of Science of the United States of America, v. 107, p. 11245-11249.

Prochnow, S.J., Nordt, L., Atchley, S., and Hudec, M.R., 2006, Multi-proxy evidence for middle and late Trassic climate trends in eastern Utah: Palaeogeography, Palaeoclimatology, Palaeoecology, v. 232, p. 53-72.

Quade, J., Cerling, T.E., and Bowman, J.R., 1989, Development of the Asian monsoon revealed by marked ecological shift during the latest Miocene in northern Pakistan: Nature, v. 342, p. 163-166.

Retallack, G.J., 1994, The environmental factor approach to the interpretation of paleosols, in Amundson, R., ed., Factors of soil formation: A fiftieth anniversary retrospective: Soil Science Society of America Special Publication 33, p. 31-64.

-, 2005, Pedogenic carbonate proxies for amount and seasonaliity of precipitation in paleosols: Geology, v. 33, p. 333-336.

-, 2009, Refining a pedogenic-carbonate CO₂ paleobarometer to quantify a middle Miocene greenhouse spike: Palaeogeography, Palaeoclimatology, Palaeoecology, v. 281, p. 57-65.

Robinson, S.A., Andrews, J.E., Hesselbo, S.P., Radley, J.D., Dennis, P.F., Harding, I.C., and Allen, P., 2002, Atmospheric pCO₂ and depositional environment from stable-isotope geochemistry of calcrete nodules (Barremian, lower Cretaceous, Wealden Beds, England): Journal of the Geological Society, London, v. 159, p. 215-224.

Romanek, C.S., Grossman, E.L., and Morse, J.W., 1992, Carbon isotopic fractionation in synthetic aragonite and calcite - effect of temperature and precipitation rate: Geochimica et Cosmochimica Acta, v. 56, p. 419-430.

Royer, D.L., 1999, Depth to pedogenic carbonate horizon as a paleoprecipitation indicator?: Geology, v. 27, p. 1123-1126.
-, 2006, CO₂-forced climate thresholds during the Phanerozoic: Geochimica et Cosmochimica Acta, v. 70, p. 5665-5675.

Schauble, E.A., Ghosh, P., and Eiler, J.M., 2006, Preferential formation of ¹³C-¹⁸O bonds in carbonate minerals, estimated using first-principles lattice dynamics: Geochimica et Cosmochimica Acta, v. 70, p. 2510-2529.

Yapp, C.J., and Poths, H., 1992, Ancient atmospheric CO₂ pressures inferred from natural goethites: Nature, v. 355, p. 342-344.

Figure 1. A graphical representation of the lever rule as applied to the paleosol barometer. δ¹³C_r* represents the diffusion-modified δ¹³C value of the soil-derived endmember and equals 1.0044δ¹³C_r + 4.4. The magnitude of [CO₂]_atm and S(z) are proportional to the distances along the lever, or differences in δ values, as labeled. Equation 1 can be written directly from the relationship shown.

Figure 2. Monte Carlo simulations of the uncertainty of calculated atmospheric CO₂ concentrations. 10,000 values were randomly selected from each of the following normal distributions (mean ± standard deviation) and used to calculate atmospheric CO₂ concentrations with equation 2: δ¹³C_r = -26 ± 1‰, δ¹³C_a = -6.5 ± 1‰, temperature = 25 ± 5°C, S(z) = 1000, 2500 or 5000 ± 50%. A range of mean δ¹³C_pc values between -3 and -12‰ (± 0.5‰) were used to calculate a range of mean atmospheric CO₂ concentrations (x-axis) for each mean S(z) value. The total uncertainty was estimated by calculating the standard deviation (1σ) of each set of 10,000 atmospheric CO₂ concentrations and is expressed as a percentage of the mean calculated value of [CO₂]_atm.

Figure 3. Monte Carlo simulations of the effect of each variable in equation 2 on the total uncertainty. The y-axis is the ratio of the uncertainty calculated when the value of one of the variables (labeled on each plot) is known exactly to the total uncertainty from Figure 2.